The Philosopher’s Stone was an elusive goal of alchemists, ostensibly capable of producing the elixir of life and transmuting lead into gold. Or maybe it was itself the elixir of life? When it comes to the ideas in alchemy, I find things to be a bit hazy (it also doesn’t help that the Philosopher’s Stone doesn’t actually exist). But unlike the Stone itself, a presumed precursor for the Stone was actually able to be made: the Philosopher’s Tree.
The Philosopher’s Tree, which I learned about in Carl Zimmer’s new book Life’s Edge, was a tree-like crystal that could be “grown” under certain conditions. As per Wikipedia:
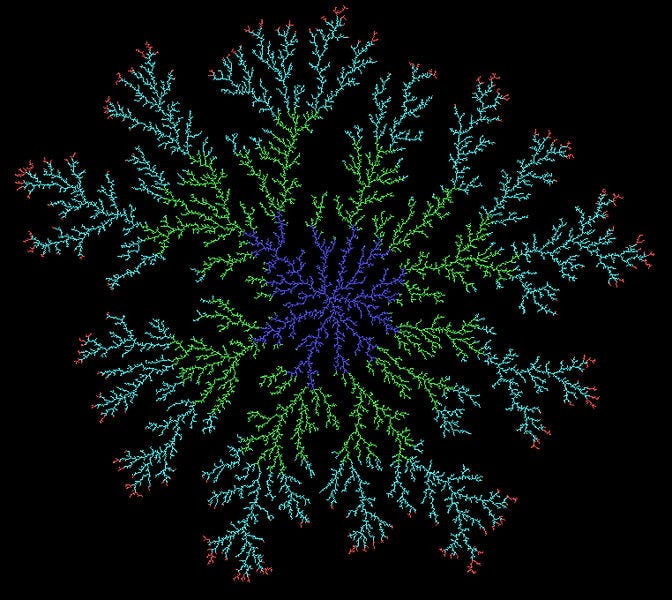
It is a dendritic amalgam of crystallized silver, obtained from mercury in a solution of silver nitrate; so-called by the alchemists, among whom “Diana” stood for silver. The arborescence of this amalgam, which even included fruit-like forms on its branches, led pre-modern chemical philosophers to theorize the existence of life in the kingdom of minerals.
Points for the use of the word “arborescence” aside, the philosopher’s tree reminds me of constructs found in the world of complexity science, especially what results from the process of diffusion-limited aggregation:
Diffusion-limited aggregation, or DLA, is the process of successive randomly-walking points aggregating together upon an original starting seed. And they are not that hard to program (I vaguely recall making one years ago using the programming language Processing).
The science writer Philip Ball has written a gorgeously illustrated book called Patterns in Nature, devoted to showing the categories of these patterns and exploring the reasons behind these ubiquitous kinds of shapes, whether cracks in a surface, fractal-like shapes, or much more.
And those in the computational realm have run with this approach, simplifying models down to their very bones and constructing computational toys powerful in their rich generative creativity, from cellular automata to falling-sand games and L-systems, each of which uses a small set of rules to generate complex and beautiful natural phenomena.
As someone who has spent lots of time in the field of complex systems, I am still entranced by this possibility (I’ve previously written about small chunks of code unspooling computational worlds). Perhaps there is even a hint of the alchemical wish here: that if we can find the set of rules and primitives, we can generate massive complexity.
And yet. The world is incredibly messy, and not everything—or even most of the world—can be fully understood by models like these. These are simplifications, powerful in their evocativeness and guides to our intuition, yet far from able to completely explain our world. L-systems can give us insight into plants, but they are not one and the same. So too with cellular automata and the patterns on shells. (This kind of complexity is discussed further in my book Overcomplicated.)
But that’s okay. As long as we realize what models are for—and how amazing and unifying they can sometimes be!—we can gain understanding and make progress. The Philosopher’s Tree never got us to the Philosopher’s Stone, but it might still teach us something about the complex field of chemistry.
I’ve been continuing to add organizations to the Overedge Catalog. If anyone has any further suggestions, please reach out. Also, the Catalog is on the verge of becoming too unwieldy for all entries to be listed on a single page, so if you have any suggestions for other modes of organization for the Catalog, please let me know.
Is the richness of the world embedded within GPT-3? Perhaps…

A few links worth checking out:
Persuading the Body to Regenerate Its Limbs: “When a caterpillar becomes a moth, most of its brain liquefies and is rebuilt—and yet researchers have discovered that memories can be preserved across the metamorphosis.” Whoa.
Mac Chimes of Death: Only the LC chime sounds familiar to me (it was quite disturbing to hear in the wild), which I guess is a good sign…
Unadversarial examples: Designing objects for robust vision: “Instead of using perturbations to get neural networks to wrongly classify objects, as is the case with adversarial examples, we use them to encourage the neural network to correctly classify the objects we care about with high confidence.”
A Revolution Is Sweeping the Science of Ancient Diseases: Contains a discussion of the extraction of DNA from teeth in old graves in order to learn about the Black Death.
Until next month.